Valuated gaussoids

For Theorem 7.1, we compute the tropical variety defined by the 18 trinomials

-a12*a23+p2*a13-p*a13t2
a12*p13-a13*a23t1-p1*a12t3
-a12*p23+p2*a12t3+a23*a13t2
a12*p3-a23*a13-p*a12t3
-a13*p23+a23*a12t3+p3*a13t2
-a23*p13+p3*a23t1+a13*a12t3
-a23t1*a12t3-p13*a13t2+a13*p123
a23t1*p23+a12t3*a13t2-a23*p123
-p1*a23+a12*a13+p*a23t1
-p1*p2+a12^2+p*p12
p1*p3-a13^2-p*p13
-p12*a12t3-a23t1*a13t2+a12*p123
-p12*a13+a12*a23t1+p1*a13t2
p12*a23-p2*a23t1-a12*a13t2
-p12*p13+a23t1^2+p1*p123
p12*p23-a13t2^2-p2*p123
-p13*p23+a12t3^2+p3*p123
-p2*p3+a23^2+p*p23

We identify linear forms in the 14 unknowns

a12, a12t3, a13, a13t2, a23, a23t1, p, p1, p12, p123, p13, p2, p23, p3

with vectors of length 14, with coordinates taken in the above order.

The tropical variety is a 3-dimensional fan modulo its 4-dimensional lineality space. The 35 rays of this fan are found in trop3-rays.txt, organized into the 5 classes labeled a,p,A,B,C.

The fan has 153 facets, represented by 147 triangles and 6 squares which are listed in trop3-facets.txt. Each of the 6 squares is represented by its 4 triangles, so the total list has length 171. For each maximal cone, we list the types of rays, which cone in the Grassmannian 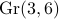it maps to, the three rays in the above list, and a representative vector in its relative interior.

The positive tropical variety in Figure 4 has 10 vertices, namely those labeled 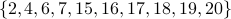above. It consists of the 16 triangles in trop3-triangles.txt.